変分問題とは、最適な関数の形を決定する問題です。一般の関数の極値問題では、関数の値が最大となるような変数の値を求めます。これに対して変分問題では、エネルギーや時間、面積などが最大／最小となるような、関数の形を求めようとする問題です。この問題は、従来の微分積分学の範囲では解を求めることができないために、「変分学」という新しい学問分野が拓かれました。

　しかし、ここで紹介するのは、当研究室で独自に考案した数値解法で、区分関数近似という手法で関数を近似することで、ディジタルコンピュータの能力・特性を最大限活用して解を求めた例です。

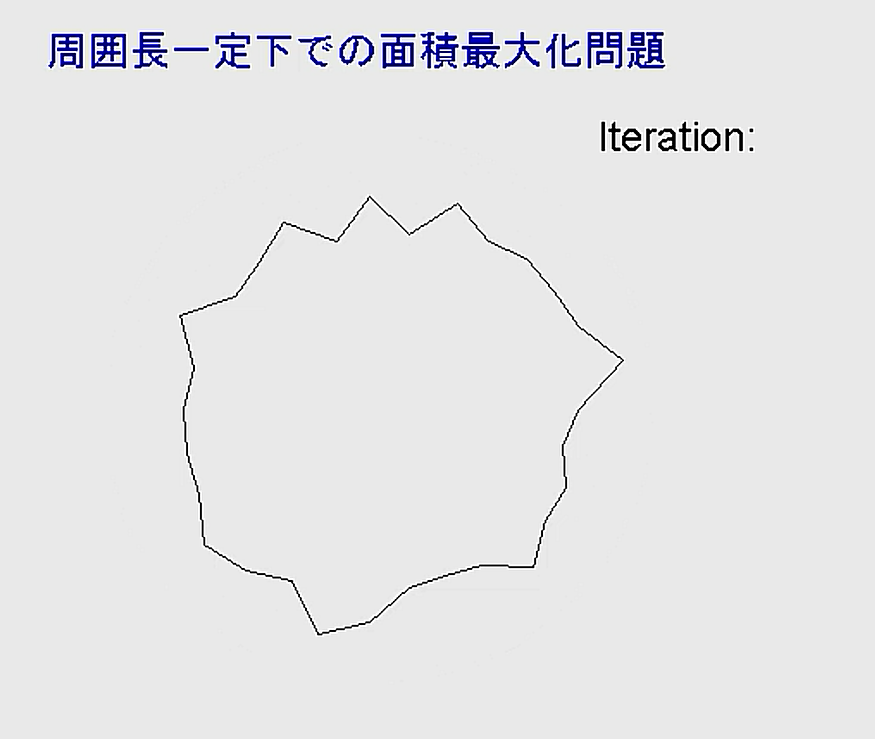
　最初の例は、等周問題ともいわれ、同じ長さのひもで最大の面積を囲むような曲線を求める問題です。正解は真円です。数値計算によって徐々に真円に近づく様子を、アニメーションでご覧下さい。

 

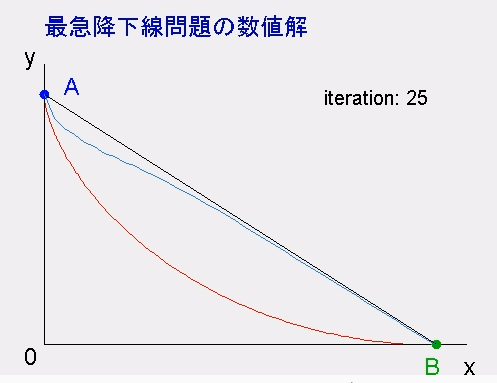
　次の例は、「最速降下線問題」です。重力のみによって、A地点からB地点までに最短時間でたどり着くような滑らかな曲線を求める問題です。正解はサイクロイド曲線です。以下の例では、区間を40分割して、曲線の近似としています。最適解（サイクロイド曲線）に近づく様子をご覧下さい。

　この手法を用いれば、、空気抵抗や摩擦がある場合のように、現実的な条件下であっても解を求めることが可能です。

 

論文：横井、数式処理システムと数値計算手法の併用による最速降下線問題および拡張問題の考察, 第29回日本シミュレーション学会大会、2010年6月.